Recall, from conditional plan evaluation, we had that:
\begin{equation} U^{\pi}(b) = \sum_{s}^{} b(s) U^{\pi}(s) \end{equation}
let’s write it as:
\begin{equation} U^{\pi}(b) = \sum_{s}^{} b(s) U^{\pi}(s) = {\alpha_{\pi}}^{\top} b \end{equation}
where \(\U_{\pi}(s)\) is the conditional plan evaluation starting at each of the initial states.
\begin{equation} \alpha_{\pi} = \qty[ U^{\pi}(s_1), U^{\pi}(s_2) ] \end{equation}
You will notice, then the utility of \(b\) is linear on \(b\) for different policies \(\alpha_{\pi}\):
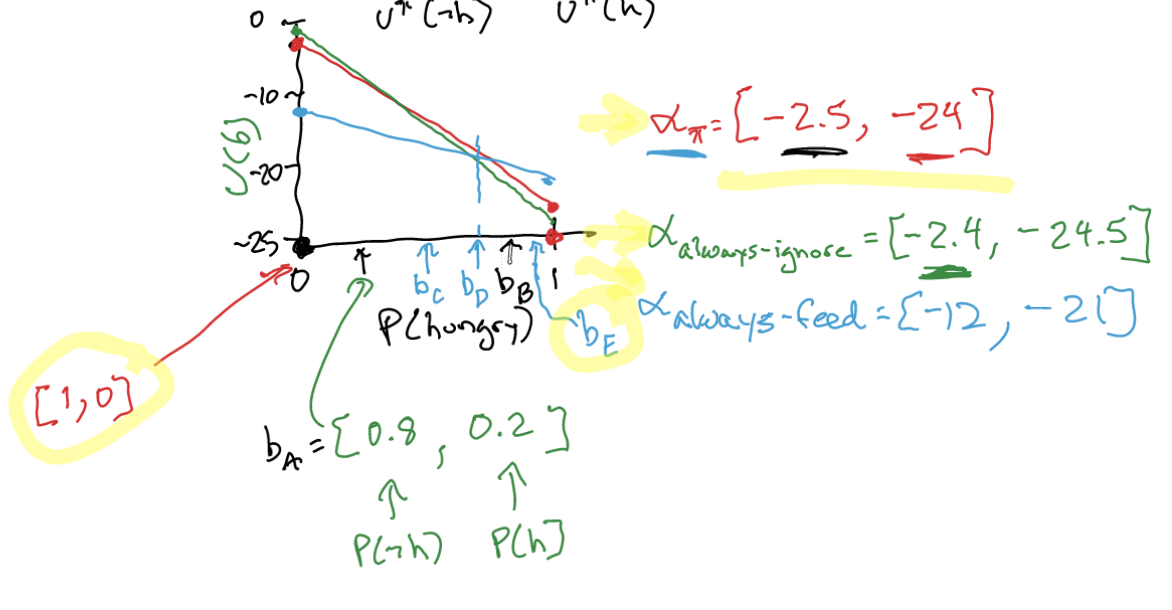
At every belief \(b\), there is a policy which has the highest \(U(b)\) at that \(b\) given be the alpha vector formulation.
Additional Information
top action
you can just represent a policy out of alpha vectors by taking the top (root) action of the conditional plan with the alpha vector on top.
optimal value function for POMDP with alpha vector
Recall:
\begin{equation} U^{*}(b) = \max_{\pi} U^{\pi}(b) = \max_{\pi} \alpha_{\pi}^{\top}b \end{equation}
NOTE! This function (look at the chart above from \(b\) to \(u\)) is:
- piecewise linear
- convex (because the “best” (highest) line) is always curving up
and so, for a policy instantiated by a bunch of alpha vectors \(\Gamma\), we have:
\begin{equation} U^{\Gamma}(b) = \max_{\alpha \in \Gamma} \alpha^{\top} b \end{equation}
To actually extract a policy out of this set of vectors \(\Gamma\), we turn to one-step lookahead in POMDP
one-step lookahead in POMDP
Say you want to extract a policy out of a bunch of alpha vectors.
Let \(\alpha \in \Gamma\), a set of alpha vectors.
\begin{equation} \pi^{\Gamma}(b) = \arg\max_{a}\qty[R(b,a)+\gamma \qty(\sum_{o}^{}P(o|b,a) U^{\Gamma}(update(b,a,o)))] \end{equation}
where:
\begin{equation} R(b,a) = \sum_{s}^{} R(s,a)b(s) \end{equation}
\begin{align} P(o|b,a) &= \sum_{s}^{} p(o|s,a) b(s) \\ &= \sum_{s}^{} \sum_{s’}^{} T(s’|s,a) O(o|s’,a) b(s) \end{align}
and
\begin{equation} U^{\Gamma}(b) = \max_{\alpha \in \Gamma} \alpha^{\top} b \end{equation}
alpha vector pruning
Say we had as set of alpha vectors \(\Gamma\):
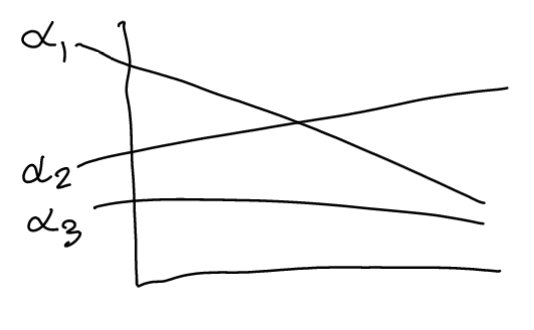
\(\alpha_{3}\) isn’t all that useful here. So we ask:
“Is alpha dominated by some \(\alpha_{i}\) everywhere?”
We formulate this question in terms of a linear program:
\begin{equation} \max_{\delta, b} \delta \end{equation}
where \(\delta\) is the gap between \(\alpha\) and the utility o
subject to:
\begin{align} &1^{\top} b = 1\ \text{(b adds up to 1)} \\ & b\geq 0 \\ & \alpha^{\top} b \geq \alpha’^{\top} b + \delta, \forall \alpha’ \in \Gamma \end{align}
if \(\delta < 0\), then we can prune \(\alpha\) because it had been dominated.
if each value on the top of the set