belief is a probability distribution over your states.
“an informational state decoupled from motivational states”
\begin{equation} b \leftarrow update(b,a,o) \end{equation}
There are two main flavours of how to represent beliefs
- parametric: belief distribution is fully represented over all states by a set of parameters (categorical, gaussian, etc.)
- non-parametric: belief is represented by a non-weighted list of possible locations of where you are; such as a Particle Filter
To update parametric beliefs, we can use a discrete state filter (for categorical belief distributions) or a Kalman Filter (for linear Gaussian). To update non-parametric beliefs, we can use a Particle Filter.
If we have an parametric belief that’s not categorical nor linear Gaussian, we can use Extended Kalman Filter or Unscented Kalman Filter to approximate a belief update.
belief update
- To update belief, we need to initialize it somehow.
- If you have no knowledge of the situation, you want to diffuse your initial distributions because you don’t want to be overconfident
- For non-parametric situations, this may cause logistical problems; so, you may need to make many observations before you can be confident enough to seed a belief
observation model
\(O(o|a,s’)\) is a model for what observations we may get if we are in a particular state/action.
error model
there is some model which is a probability distribution over the state given observation:
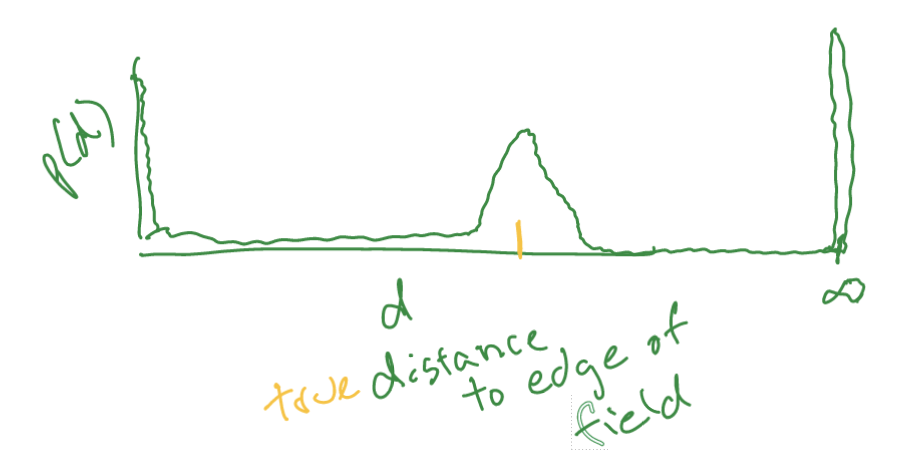
let orange \(d\) be state, the green would be the error model
filters
filters are how beliefs are updated from observation. “we want to perform localization”