combinator is a variable free programming language; it is a turing complete computational formalism.
- this is a language of functions
- it is extremely minimalist
- clear away the complexity of a real language
- allows for illustration of ideas
combinator
a combinator is a function with no free variables
Why do we care?
- no variables! its entirely compositional
- all computations are rewrite rules => making proofs like confluence, etc. easier
- its functional: we don’t reason about individual data accesses, which is a natural fit for bulk and parallel data
- …variables are often a problem is parallel computation
Why do we not care?
Duplication is really hard in SKI; we had to use \(S\) and possibly a \(K\) to get multiple thing to be passed. This is basically the only way we can pass information around—we have to drill any data all the way down with \(S\) until you consume it
this doesn’t really match the way we build computers—memories exist.
definition
Terms of SKI calculus are the smallest sets such that \(S, K, I\) are terms; and if \(x, y\) are terms, then \(x y\) is a term.
key fact: terms are trees, not strings—in absence of parans, association is to the left: \(S x y z \to (((Sx) y) z)\)
rewrite system
- \(I x \to x\), identity function
- \(K x y \to x\), constant functions
- \(S x y z \to (xz) (yz)\), generalized function application
Constant formating function \(K\)
\(K\) semantics:
- \(K\), pass; doesn’t cause computation
- \(Kx\), partial function application; doesn’t cause comptation
- \(K x y \to x\), only executes when it has two arguments
- \(K x y z \to x z\), again a partial application
this is a constant-forming function, meaning apply \(x\) to \(K\) will give you the constant \(x\), no mater what else ouo do to it
function application \(S\)
this allows you to—
- have fnction calls
- reuse values
\begin{equation} S x y z \to (xz) (yz) \end{equation}
CFG
- \(Expr \to S\)
- \(Expr \to K\)
- \(Expr \to I\)
- \(Expr \to Expr Expr\)
- \(Expr \to (Expr)\)
- \(Expr \to S | K | I | Expr Expr | (Expr)\)
\(Expr\) is a non terminal; CFG application is done when we have no more \(Expr\) left.
abstraction algorithm
the abstraction algorithm is a system for writing out combinators.
- start with a function equation using the variables we want \(swap\ x y \to y x\)
- then, use an abstraction algorithm \(A\) which eliminates variables on RHS and replace them with \(S, K, I\)
key: run this algorithm in the currying order; so if we have $f x y = …$, run \(A\) on \(y\) first, then \(x\)
\(A(b,a)\) is an algorithm that drops a from the expression b. consider: \(f x = E\), we want a combinator that does \(A(E,x)\) which implements \(f\).
- \(A(x,x) = I\)
- \(A (E, x) = K E\), if \(x\) is not in \(E\)
- \(A ( E_1 E_2, x) = S A(E_1, x) A (E_2, x)\)
(non standard) Alex’s special abstraction rules
define:
\(c_1 x y z \to x ( y z)\)
\(c_2 x y z = (x z) y\)
\(A(E_1 E_2, x) = c_1 E_1 A (E_2, x)\), if \(x\) doesn’t appear in \(E_1\)
\(A(E_1 E_2, x) = c_2 A (E_1, x) E_2\) , if \(x\) doesn’t appear in \(E_2\)
\(A(E_1 E_2, x) = S A(E_1, x) A(E_2, x)\), otherwise
For each variable on the right time, we want to apply the abstraction algorithm \(A\) once: an example with \(swap\ x y \to y x\)
- \(yx = A(y x, y) = S A (y,y) A(x,y) = SI (K x)\)
- \(SI (K x) = A(SI (K x), x)\) and so on
we apply \(A\) in the currying order, meaning for \(f x y z\), we apply \(A\) first on \(z\), then \(y\), and \(x\). It is essentially defining \(SKI\) in reverse.
programming with SII calculus
general recursion
Notice that \((SII)(SII) \to I (SII) I(SII) \to (SII) (SII)\) is a basic infinite loop. suppose we want to keep applying \(f\) to something.
Let us define \(x = S(Kf)(SII)\).
So now:
\begin{equation} S II x \to^{*} x x \to^{*} f (x x) \to^{*} f(f(x x)) \dots \end{equation}
general tip: notice apply \(K\) to things is a good way to get more of that thing. We use that trick in \(x\)
expanding one step
\(x x \to S (Kf) (S II ) x \to S (K f) x ( S I I) x\)
conditionals
Let’s first create some encoding (weak “ADT” without type system) which gives you booleans. Perhaps we can design true and false such that \(T a b \to a\) and \(F a b \to b\).
- \(T = K\)
- \(F = SK\)
Now, we also need to create our boolean operations:
- not: \(B F T\) because if \(B\) is true, it will pick the first thing which is a False; otherwise, it will pick the second thing which is a True
- or: \(B_1 T B_2\) because if \(B_1\) is true, it will give you \(T\), otherwise, it will give you what \(B_2\)
- and: \(B_1 B_2 F\) because if \(B_1\) is true, we also need \(B_2\) to be true; otherwise, it will give you False
If statements:
- \(B X Y\), because our boolean is the thing that allows us to choose between branches
pair
pair is 2-tuples:
- \(pair\ x y\ first = x\)
- \(pair\ x y\ second = y\)
let us choose
- \(first = T\)
- \(second = F\)
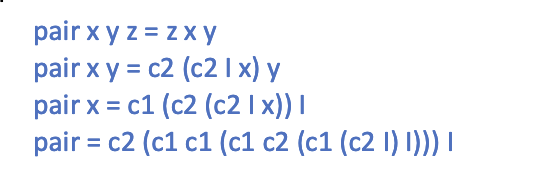
natural numbers
natural number \(n\) is a function that applies its first argument \(n\) times to the second arguments, meaning:
- \(0 f x = x\); so \(0 = S K\)
- \(succ\ n f x = f (n f x)\); so \(succ = S(S (K S) K)\)
some operations
- \(1 = succ\ 0\)
- \(add\ x y = x\ succ\ y\)
- \(mul\ x\ y = x\ (add\ y)\ 0\)
you will note that this is primitive recursion: the number of times we iterate is fixed (or capped, as in break) on entry—we cannot use control flow to stop recursion.
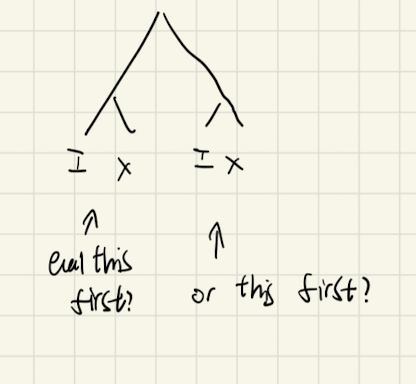
Reduction Order
When do we actually apply the reduction? As in, when and how do we apply the rewrites?
in a large expression, many rewrite rules may apply
so how do we choose when to actually evaluate?
The process for choosing where to apply the rules is a reduction strategy—most languages have a fixed reduction/evaluation order. However, concurrent programming/parallel do provide multiple choices.
one place in C where the evaluation order is not specified
f(x+1, y*3)
its not specified if we evaluate the arguments left to right or right to left. This causes a problem, say in globals. Suppose you had:
int z;
f(g(x), h(y));
suppose with side effects g changes z, and h reads z. The evaluation order, then, change the read order.
a good reduction strategy: normal order
normal order
- traverse the leftmost spine of the expression tree from root to the leaf
- if a rewrite rule applies (i.e. backup enough rules to get your arguments, etc.), apply it, repeat
- otherwise, halt (yes, this can leave things unevaluated, but so does
f() { x+y }without callingf)
this is also called lazy evaluation — only evaluates what is absolutely necessary to get an answer; if any reduction order terminates, normal order will terminate
other languages mostly call by value instead of lazy order (except Haskall).
what could go wrong if you don’t use normal order?
no! confluence: SKI exhibits one-step diamond property
Examples
- \(SK xy \to (K y) (x y) \to y\) — so the function \(SK\) returns the second argument
- \(K x y \to x\) — so the function \(K\) returns the first argument
- \(S II X \to (Ix) (Ix) \to x (I x) \to x x\)
- \((SII)(SII) \to I (SII) I(SII) \to (SII) (SII)\) — infinite loop
- swap: \(swap\ x y \to y x\) is defined by \(swap = S ( K ( SI)) (S (K K) I)\)
factorial
Let’s write it out first:
- \(fac\ n = fac’\ 1\ 1\ n\)
- \(fac’\ a\ i\ n = if\ i > n\ then\ a\ else\ fac’\ (a * i) (i + 1)\ n\)
[TODO]