a controller is a that maintains its own state.
constituents
- \(X\): a set of nodes (hidden, internal states)
- \(\Psi(a|x)\): probability of taking an action
- \(\eta(x’|x,a,o)\) : transition probability between hidden states
requirements
Controllers are nice because we:
- don’t have to maintain a belief over time: we need an initial belief, and then we can create beliefs as we’d like without much worry
- controllers can be made shorter than conditional plans
additional information
finite state controller
A finite state controller has a finite amount of hidden internal state.
Consider the crying baby problem. We will declare two internal state:
\begin{equation} x_1, x_2 \end{equation}
Given our observations and our internal states, we can declare transitions and an action probability \(\Psi\):
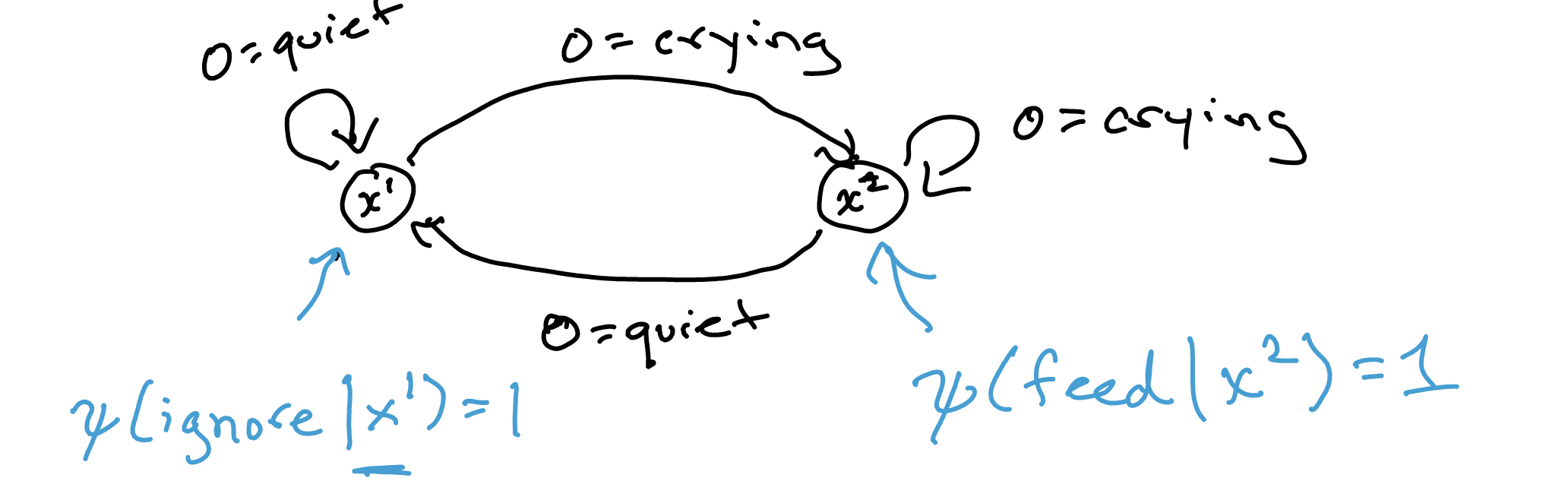
We essentially declare a policy vis a vi your observations. It can be a sequence, for instance, if we want to declare a policy whereby if you cry twice then you feed, you can declare:
finite state controller evaluation
\begin{equation} U(x, s) = \sum_{a}^{} \Psi(a|x) \qty[R(s,a) + \gamma \qty(\sum_{s’}^{} T(s’|s,a) \sum_{o}^{} O(o|a, s’) \sum_{x’}^{} \eta(x’|x,a,o) U(x’, s’)) ] \end{equation}
which is a conditional plan evaluation but we know even litle
and, to construct alpha vectors:
\begin{equation} \alpha_{x} = \qty[U(x, s_1), \dots, U(x, s_{n})] \end{equation}
we just make one alpha vector per node. So the entire plan is represented as usual by \(\Gamma\) a set of alpha vectors. And yes you can alpha vector pruning.
\begin{align} U(x,b) = b^{\top} \alpha_{x} \end{align}
node we want to start at:
\begin{equation} X^{*} = \arg\max_{x} U(x,b) \end{equation}
solving for \(\Psi\) and \(\eta\)
- policy iteration: incrementally add nodes and evaluate it
- nonlinear programming: this can be a nonlinear optimization problem
- controller gradient ascent