dynamic programming

dynamic programming is a three-step algorithm to tackle large, multi-step problems; high level idea: guessing + caching + recursion.

dynamic programming can sometimes not be good enough, and it doesn’t really give us fast enough to get what we need to use. That’s when we need to deal with relaxation, or possibly greedy programming.

main steps of dynamic programming

1. Break a hard problem into sub-problems
2. Guess what sub-problem to solve
3. Solve the sub-problem and store the solution
4. Repeat #2 and #3
5. Combine sub-problem solutions to solve the hard problem

analyzing runtime of dynamic programming

To analyze runtime of dynamic programming problems, you ask:

• How many sub-problems are there?
• How long does it take to solve each sub-problem?
• How long does it take to combine sub-problems?

fibonacchi numbers: dynamic programming

here’s an example top-down dynamic programming problem:

1. There are \(n\) sub-problems: \(F_1, F_2, \ldots, F_{n-1}\).
2. Solve a sub-problem, then store the solution
   1. \(F_{n-1} = F_{n-2}+F_{n-3}\)
   2. Continue until \(F_1 =1\).
3. Now, we can recurs back up (popping the call stack) and cache all calculated results
4. So then we can just look up any \(F_k\).

shortest path: dynamic programming

here’s a graph! how do we get to node \(6\)?

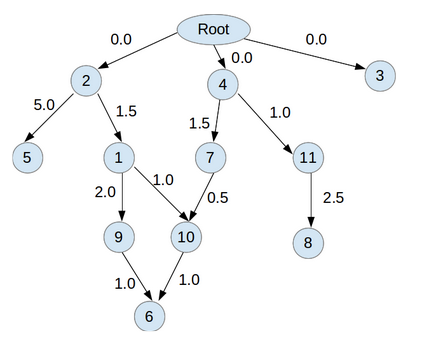
1. Guess that the shortest path goes through 10
2. Go recursively until you get to root, cache the solution
3. Do it again until you got to all subproblems
4. Look up cached result