inference is the act of updating the distribution of a random variable based on distribution of actually observed variables:
\begin{equation} P(X|Y) \end{equation}
where \(Y\) is observed, and we want to know how likely \(X\) would therefore be.
We call the set \(X\) the “query variables”, \(Y\) as “evidence varibales”, and anything that we didn’t use which connects the two variables as “hidden variables”.
If things are not in the right order of \(X\) and \(Y\), consider the Bayes rule.
Inference is Hard
- mix of continuous and discrete distribution
- results could be either a PMF or a PDF
Example
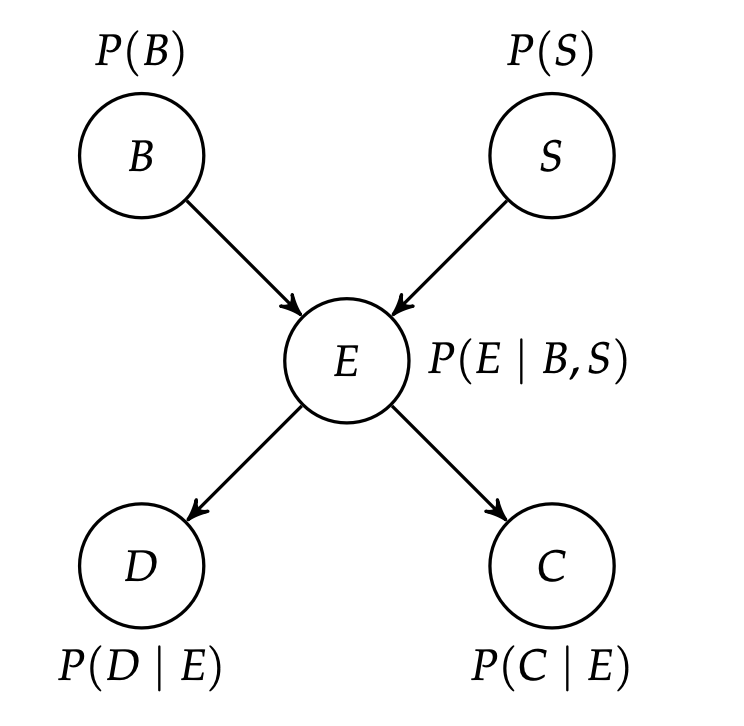
Suppose we’d like to know \(P(b^{1} | d^{1}, c^{1})\), where \(b^{1}\) is considered a query variable, and \(c^{1}\) is considered evidence varibales. The definition of the conditional probability gives us:
\begin{equation} p(b^{1} | d^{1}, c^{1}) = \frac{p(b^{1}, d^{1}, c^{1})}{p(d^{1}, c^{1})} \end{equation}
To compute \(p(b^{1}d^{1}c^{1})\), we first compute:
\begin{equation} p(b^{1}, d^{1}, c^{1}, E, S) \end{equation}
and then, use the law of total probability to get:
\begin{equation} p(b^{1}, d^{1}, c^{1}) = \sum_{e=E} \sum_{s=S} p(b^{1}, d^{1}, c^{1}, E, S) \end{equation}
you will note this is very expensive computationally O(es) — and if you have like a 1000 hidden variables you will die.
We therefore introduce sum-product elimination.
sum-product elimination
You will note the summation in the example above has a lot of interlocking for loops. You can “factor them out” via the sum-product elimination algorithm.
Suppose you are interested in:
\begin{equation} P(b | d’, c’) \end{equation}
Step 1: write down factors
Write down all factors associated with this computation:
\begin{equation} \phi_{1}(B), \phi_{2}(S), \phi_{3}(E,B,S), \phi_{4}(D,E), \phi_{5}(C,E) \end{equation}
we have evidence at two variables: \(D, C\).
Step 2: performing factor conditioning for all evidence variables
Therefore, \(\phi_{4}\) and \(\phi_{5}\) can be replaced by the factor conditioning as we observed \(d, c\), so we no longer need \(d, c\) as input because we know them:
now we have, to replace \(\phi_{4}, \phi_{5}\):
\begin{equation} \phi_{6}(E), \phi_{7}(E) \end{equation}
Step 3: using the law of total probability and factor product, get rid of hidden variables
We then choose an ordering of the hidden variables and apply a factor product using the law of total probability to get rid of them:
- First get rid of any hidden variables
- Then use factor product to combine results
\begin{equation} \phi_{8}(B,S) = \sum_{E=e} \phi_{3}(E,B,S) \phi_{6}(e) \phi_{7}(e) \end{equation}
\begin{equation} \phi_{9}(B) = \sum_{S=s} \phi_{2}(s) \cdot \phi_{8}(B,S) \end{equation}
We now only have two factors left: \(\phi_{1}(B)\phi_{9}(B)\). We finally apply factor product again:
\begin{equation} \phi_{10} (B) = \phi_{9}(B) \cdot \phi_{1}(B) \end{equation}
