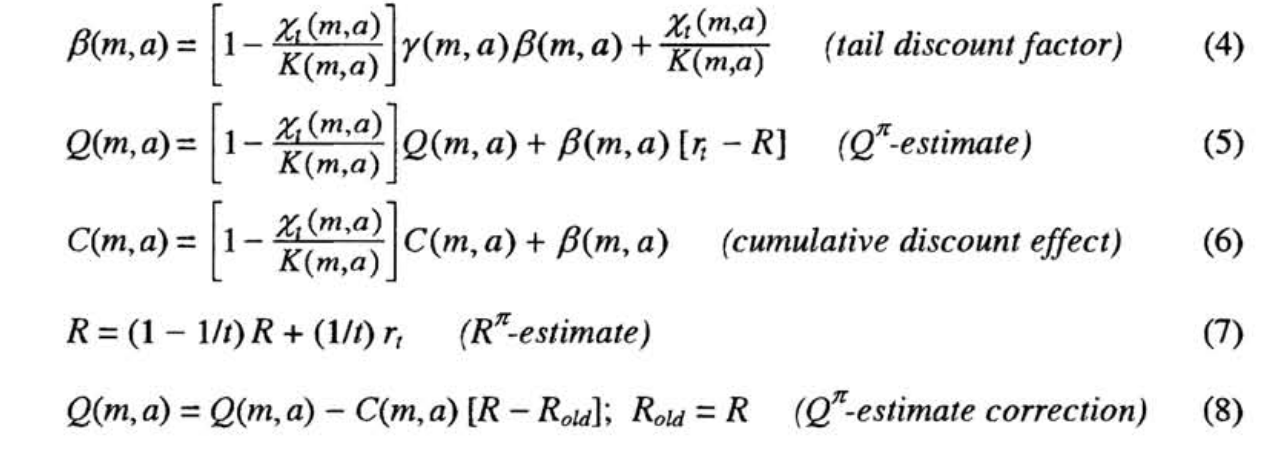JSJ

POMDPs can become computationally quite intractable. Alternative: a stochastic, memoryless policy. A policy should be stochastic in order to satisfy certain conditions during adversarial games (think bluffing).

JSJ is basically Q-Learning adapted for POMDPs:

\begin{equation} \begin{cases} Q^{\pi}(s,a) = \sum_{t=1}^{\infty}\mathbb{E}_{\pi} [r_{t}- R^{\pi}|s, a] \\ Q^{\pi}(o,a) = \mathbb{E}_{s}[Q^{\pi}(s,a) | M(s) = o] \end{cases} \end{equation}

where \(M\) is a mapping between states and possible observations.

Policy Improvement

Now, we want to maximise:

\begin{equation} \Delta_{o}(a) = Q(o,a) - V(o) \end{equation}

“if an action \(a\) results in a better value than the expected value, we want to upweight that action.”

We further normalise this:

\begin{equation} \delta_{o}(a) = \Delta_{o}(a) - \frac{1}{|A|} \sum_{a’ \in A} \Delta_{o}(a’) \end{equation}

“how does the diff of my action is considering improve over all other actions (i.e. “maybe all actions have similar diffs”).

Now, substitution time:

\begin{equation} \delta_{o}(a) = \qty(Q(o,a) - V(o)) - \frac{1}{|A|} \sum_{(a’ \in A)} Q(o,a’) - V(o) \end{equation}

Which, after simplification (the two \(V\) cancels out), we actually get:

\begin{equation} \delta_{o}(a) = Q(o,a) - \frac{1}{|A|} \sum_{(a’ \in A)}^{} Q(o,a’) \end{equation}

which makes sense; “how does our current action does better than all others”. To obtain \(Q(o,a)\), see the big function above.

Finally, having defined our update step, we can now let the good times roll—-gradient ascent! For some action \(a\) at observation \(o\) and learning rate we update our policy:

\begin{equation} Q^{\pi}(a|o) = Q^{\pi}(a|o) + \varepsilon \delta_{o}(a) \end{equation}

We can then use it to take some more actions, compute more deltas, repeat.

Policy Evaluation