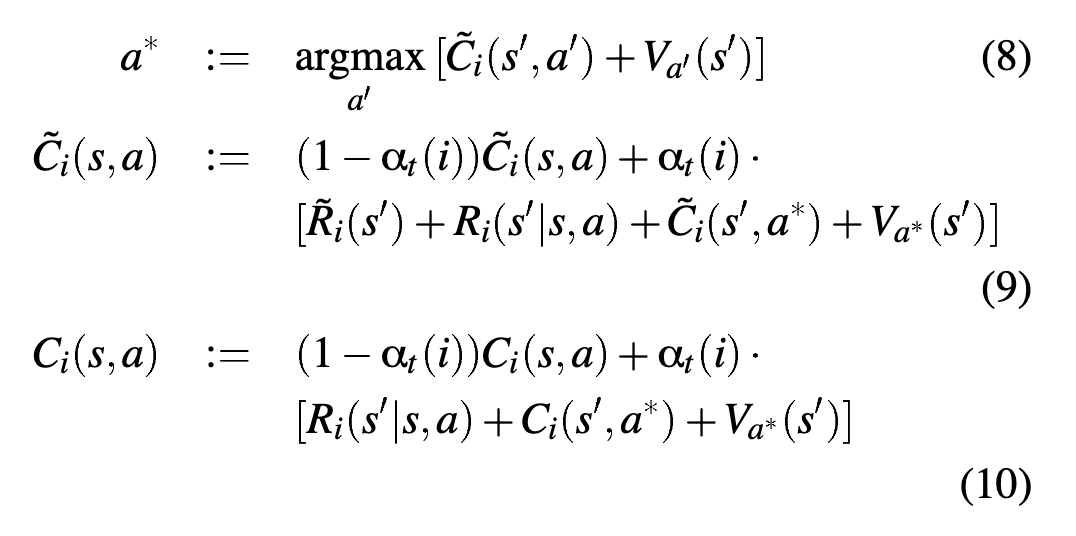Two Abstractions
- “temporal abstractions”: making decisions without consideration / abstracting away time (MDP)
- “state abstractions”: making decisions about groups of states at once
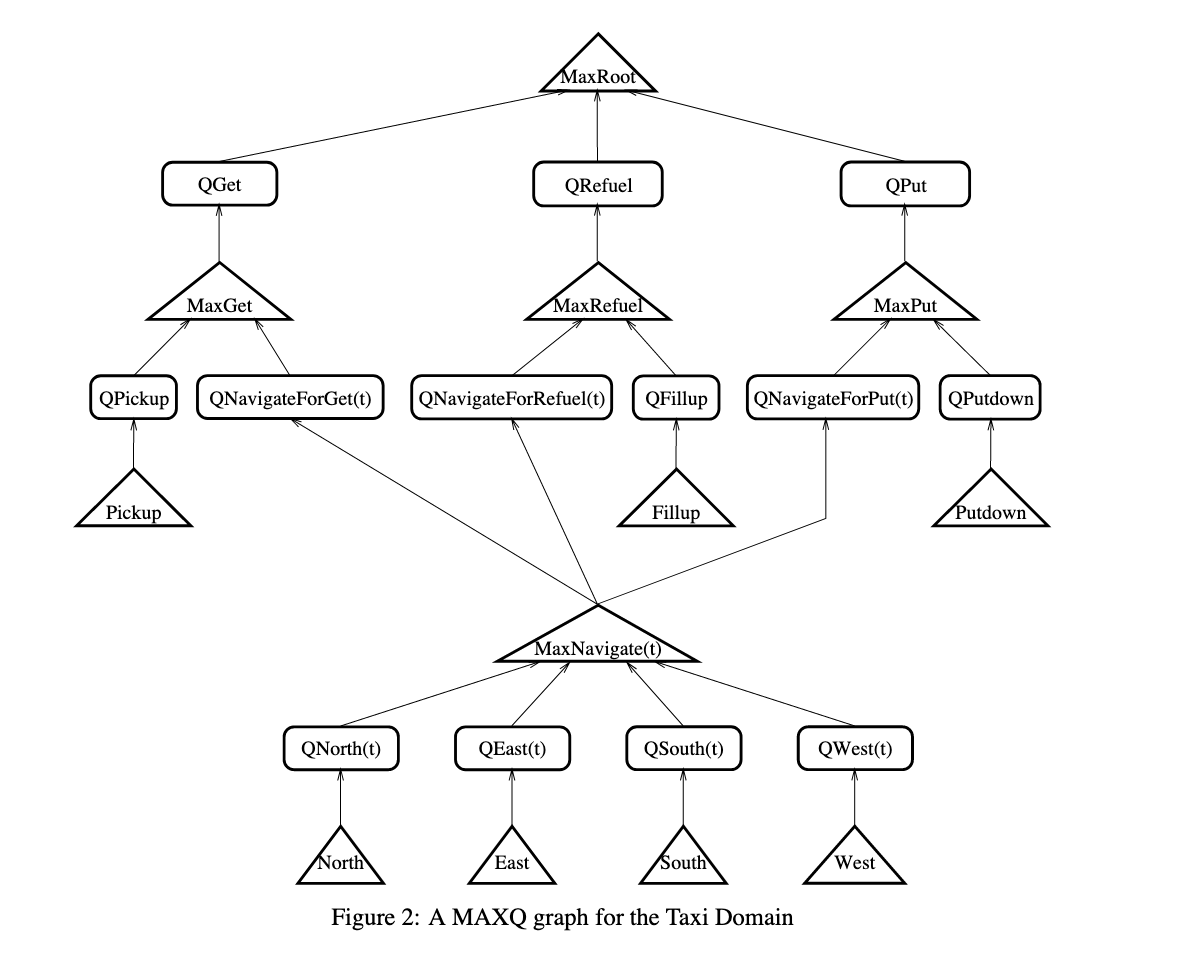
Graph
MaxQ formulates a policy as a graph, which formulates a set of \(n\) policies
Max Node
This is a “policy node”, connected to a series of \(Q\) nodes from which it takes the max and propegate down. If we are at a leaf max-node, the actual action is taken and control is passed back t to the top of the graph
Q Node
each node computes \(Q(S,A)\) for a value at that action
Hierachical Value Function
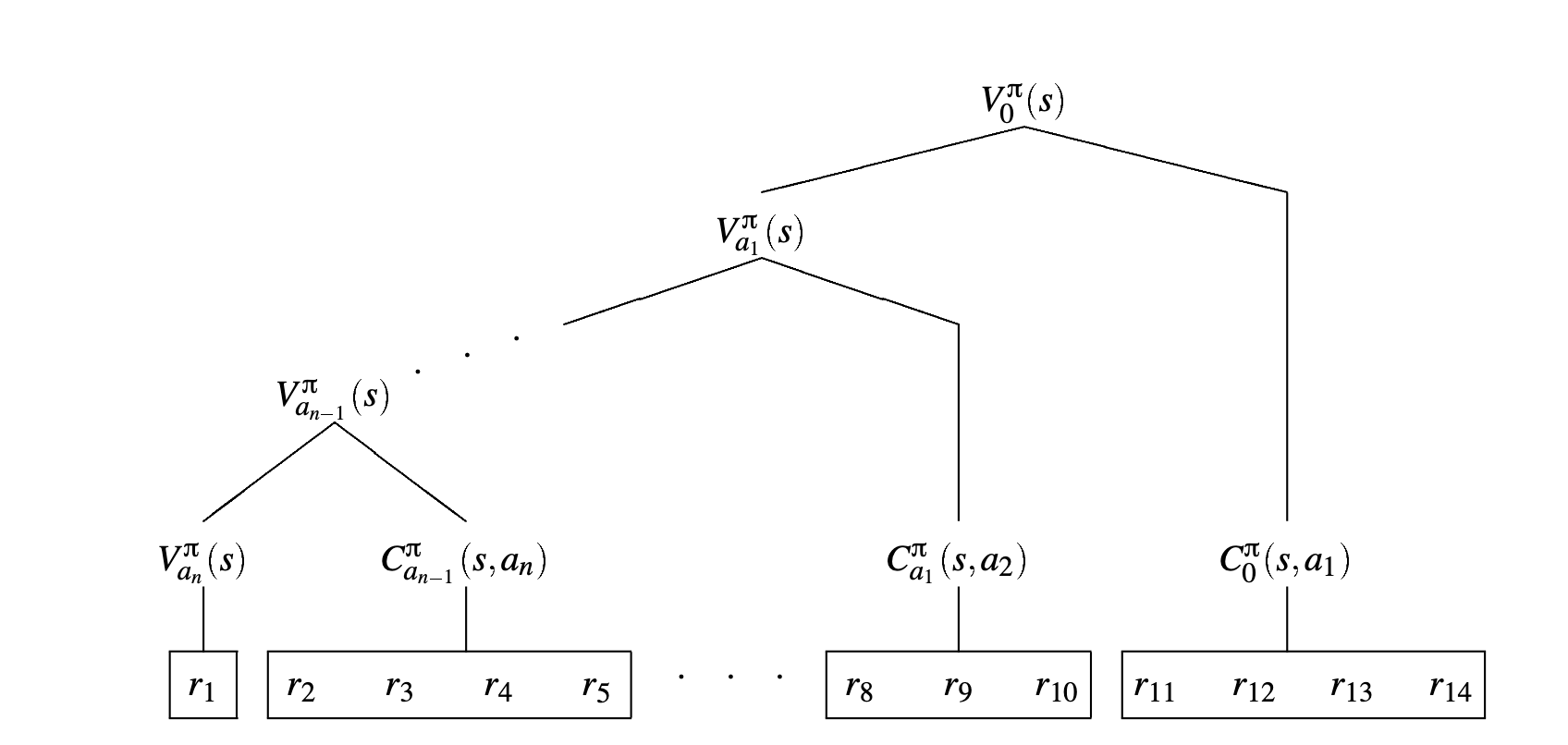
\begin{equation} Q(s,a) = V_{a}(s) + C_{i}(s,a) \end{equation}
the value function of the root node is the value obtained over all nodes in the graph
where:
\begin{equation} C_{i}(s,a) = \sum_{s’}^{} P(s’|s,a) V(s’) \end{equation}
Learning MaxQ
- maintain two tables \(C_{i}\) and \(\tilde{C}_{i}(s,a)\) (which is a special completion function which corresponds to a special reward \(\tilde{R}\) which prevents the model from doing egregious ending actions)
- choose \(a\) according to exploration strategy
- execute \(a\), observe \(s’\), and compute \(R(s’|s,a)\)
Then, update: