mutual information a measure of the dependence of two random variables in information theory. Applications include collocation extraction, which would require finding how two words co-occur (which means one would contribute much less entropy than the other.)
constituents
- \(X, Y\) random variables
- \(D_{KL}\) KL Divergence function
- \(P_{(X,Y)}\) the joint distribution of \(X,Y\)
- \(P_{X}, P_{Y}\) the marginal distributions of \(X,Y\)
requirements
mutual information is defined as
\begin{equation} I(X ; Y) = D_{KL}(P_{ (X, Y) } | P_{X} \otimes P_{Y}) \end{equation}
which can also be written as:
\begin{equation} I(X:Y) = H(X) + H(Y) - H(X,Y) \end{equation}
where \(H\) is entropy (recall that \(H(X,Y) \leq H(X)+H(Y)\) always.
“mutual information between \(X\) and \(Y\) is the additional information contributed by the "
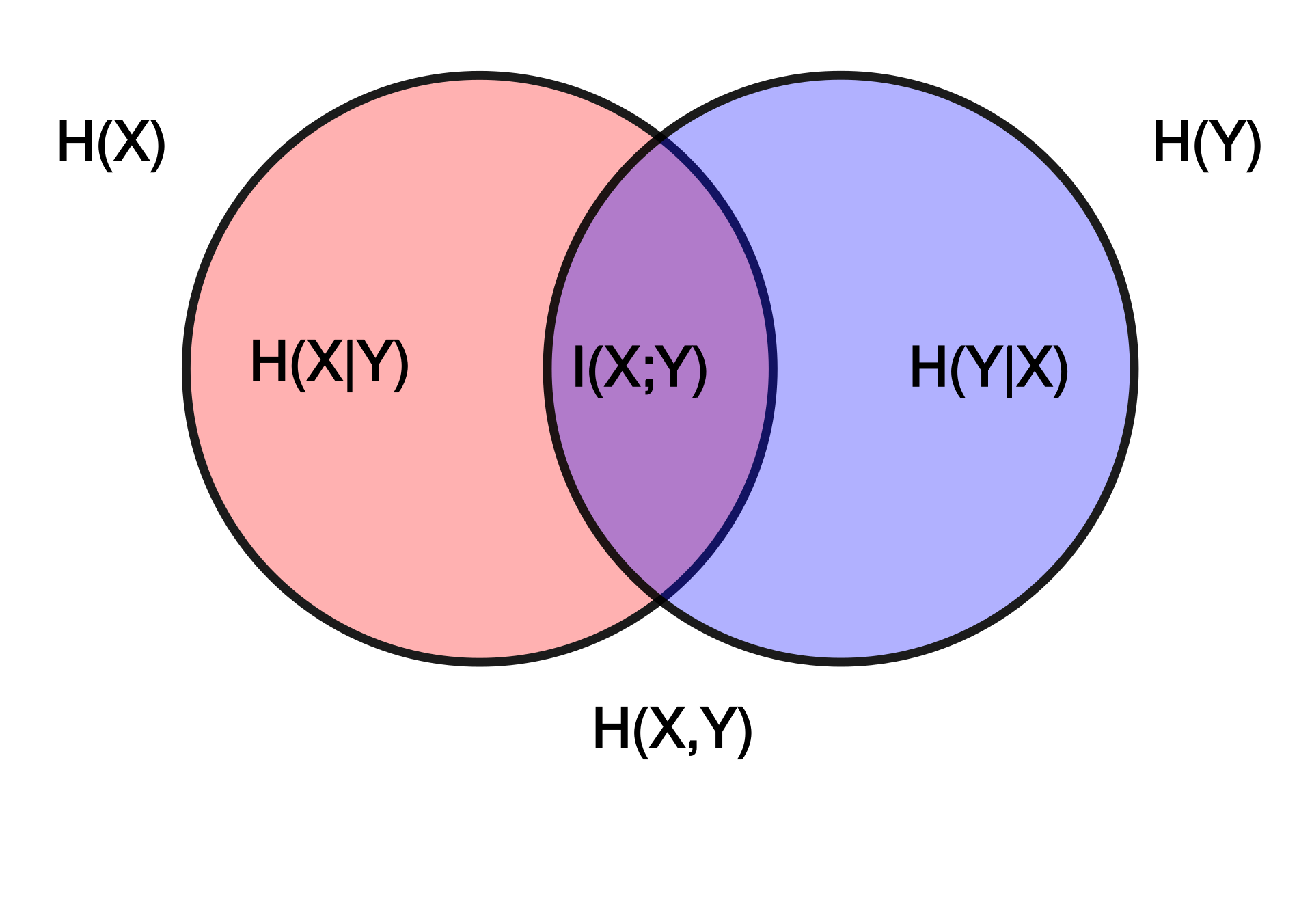
additional information
mutual information and independence
- if \(X \perp Y\), then \(H(X)+H(Y) = H(X,Y)\), so \(I(X:Y) = 0\)
- otherwise, we have \(I(X:Y) > 0\)
This is important because