NP-Complete

A language $B$ is NP-Complete if $B \in NP$ and we have that every $A \in NP$ has $A \leq_{P} B$ with a polynomial time mapping reduction. We say $B$ is NP-Hard if the reduction exists, and NP-Complete if $B \in NP$ too.

Suppose a language $L$ is NP-Complete, we have that every other language in $NP$ is mapping reducable to $L$. So, if $L \in P$, then $P= NP$, if $L \not\in P$, then $P \neq NP$.

There are thousands of NP-complete problems, most areas of science has NP-complete problems.

Corollaries

Suppose $L$ is NP-complete; then, assuming $P \neq NP$, then $L$ is not decidable in any polynomial time $n^{k}$ time for every $k$.

Show something is NP-Complete

Show that something is NP-Hard
Show that it is in NP

for a particular problem $\Pi \in NP$, we want to find some known NP-Hard thing named $\Sigma$ like 3SAT and show that $\Sigma \leq_{p} \Pi$.

many, many NP-Complete things

clique problem

Given a graph $G$ and positive $k$, does $G$ contain a complete subgraph on $k$ nodes.

\begin{equation} \text{CLIQUE} = \qty {\qty(G,k) \mid \text{$G$ is an undirected grauph with a $k$ clique}} \end{equation}

where clique is a subgraph where all possible edges are connected.

Proof:

We want to transform a 3cnf-formula $\phi$ into $(G,k)$. Let $C_1, …, C_{m}$ be the clauses of $\phi$; we want to assign $k=m$; we make a graph $G$ with $m$ groups of $3$ nodes each (i.e. 3 variables).

Construction:

Each group $i$ corresponds to clause $C_{i}$ of $\phi$, and each node in group $i$ is labeled with a literal of $C_{i}$.

We will then put edges between all pairs of nodes in different groups, except pairs of nodes with labels $x_{i}$ and $\neg x_{i}$ (that is, we connect groups unless they form a contradiction; meaning if there is an edge that means there is an assignment that satisfies both literals.) We put no edges between nodes in the same group.

Now, notice that since there no edges within a group, any cliques will be of maximally size 3. Any clique of size three will represent a satisfying assignment across the clauses since each 3cnf clause only requires one member of each group to be satisfied (within the groups, we have or statements).

A similar argument can be shown by the opposite side as well.

Actual proof:

$\Rightarrow$

Given a satisfiable assignment $A$ of $\phi$, for every clause $C$ there is at least one literal in $C$ that is set true by $A$.

For each clause $C$, let $v_{c}$ from group $C$ whose label is a literal is set true by $A$. The claim here is that $S = \qty {v_{C} \mid C \in \phi, v_{C}=1}$ is an $m$ clique.

This is because if $\qty(v_{c}, v_{c’}) \not\in E$, when $v_{c}$ and $v_{c’}$ are inconsistent. But then, since they are in different groups, we know that assignment $A$ can’t satisfy both. So there must be an edge between $\qty(v_{c}, v_{c’})$.

$\Leftarrow$

Suppose $S$ is a set of nodes which forms a $m$ clique of $G$. Let us assign some variable $x \in \phi$ to $1$ IFF there is a vertex $v \in S$ with label $x$.

For all $i = 1… m$, at least one vertex from the group $i$ is in $S$ because we have $m$ different nodes connected together by this clique, and we are not allowed to connect two nodes in the same group together.

independent set

Given a graph $G= \qty(V,E)$ and integer $k$, is there a $S \subseteq V$ such that $|S| = k$ and no two vertices in $S$ have an edge?

Recall that CLIQUE is that all edges in the verticies $S$ exists; we want to show the dual whereby no edges in $S$ exists.

We want to build this reduction

\begin{equation} CLIQUE \leq_{p} IS \end{equation}

We do this by reverse the edge/non-edge (where there is an edge, get rid of it; where there is no edge, add it).

vertex cover

A “vertex cover” is the set of nodes $C$ that cover all edges; that is, for all edges, at least one endpoint is in $C$.

\begin{equation} VC = \qty {(G,k) \mid G \text{ is a graph with a vertex cover of size at most $k$ }} \end{equation}

we can check if something is a vertex cover within $P$ time by checking all the vertices, and that means that $VC \in NP$.

We now want to write a reduction:

\begin{equation} IS \leq_{p} VC \end{equation}

The insight: $S$ is an independent set IFF $V-S$ is a vertex cover (because the verticies have to be connected everywhere else for the set $S$ to be independent).

subset sum

Given a sequence (i.e. stuff can repeat):

\begin{equation} S = \qty {a_1, \dots, a_{n}} \end{equation}

of positive integers and a positive $t$, is there an $A \subseteq \qty {1, \dots, n}$ such that $t = \Sum_{i \in A} a_{i}$.

(i.e. does any subset sum up to $t$)

We now want to reduce this problem to a vertex cover problem.

Given a graph $(G,k)$, let’s define some set $E = \qty {e_0, \dots, e_{m-1}}$ and $V = \qty {1, \dots n}$ representing edges and nodes.

We now label the edges and nodes with the following numbers:

edge labels: for $e_{j} \in E$, label $b_{j} = 4^{j}$
node labels: for every $i \in V$, label $a_{i} = 4^{m} + \sum_{j \in e_{j}}^{4^{j}}$
target $t$ for subset sum: $t = k \cdot 4^{m} + \sum_{j=0}^{m-1}\qty(2 \cdot 4^{j})$

Note that there’s an algorithm for this in $O\qty(nt)$, which isn’t showing $P=NP$ because we need it to be polynomial in input which is $n+t$.

This is $NP$ itself because the witness to success is just the set of numbers that correctly match; and now, we want to show that this is NP hard through another reduction.

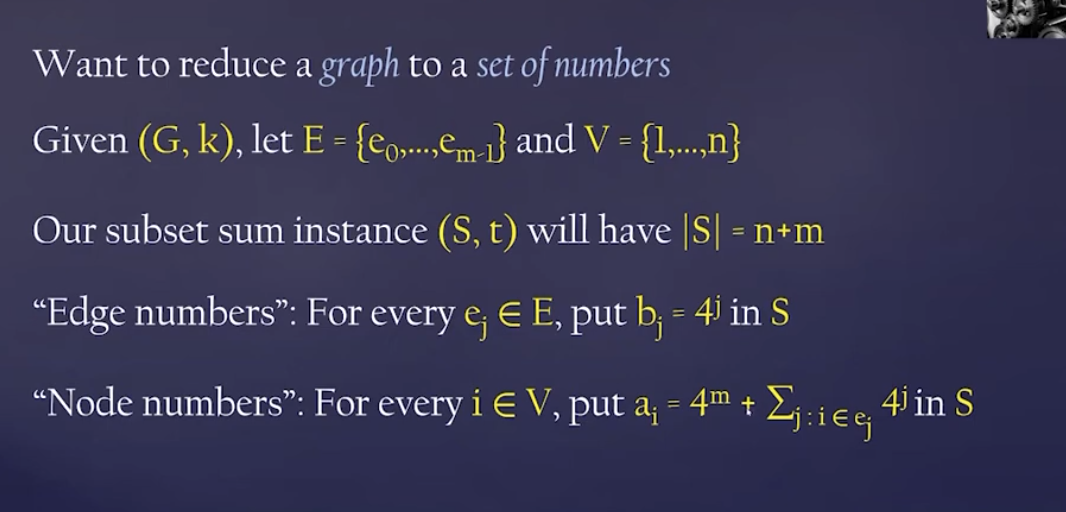
Hamiltonian path problem

Hamiltonian path problem is NP complete through 3SAT

shortest path

where simple path is a path going through each node at most once:

SHORTEST (this is in polynomial time):

\begin{equation} \qty {\qty(G, s,t,k) \mid G\text{ has a simple path of length $<k$ from $s$ to $t$}} \end{equation}

LONGEST (this is NP-complete):

\begin{equation} \qty {\qty(G, s,t,k) \mid G\text{ has a simple path of length $<k$ from $s$ to $t$}} \end{equation}

HAMPATH <= LONGEST-PATH (because (gst) in HAMPATH = (gst |V|) in LONGEST) — getting a simple path of length |v| which is all verticies can only happen if you touch each vertex exactly once.