\begin{equation} \text{PH} = \bigcup_{c \in \mathbb{N}} \Sigma_{c} = \bigcup_{c \in \mathbb{N}} \pi_{c} \end{equation}
“a language is in the polynomial hierarchy if it can be described with a constant number of qualifiers”
results and conjectures
polynomial hierarchy conjecture
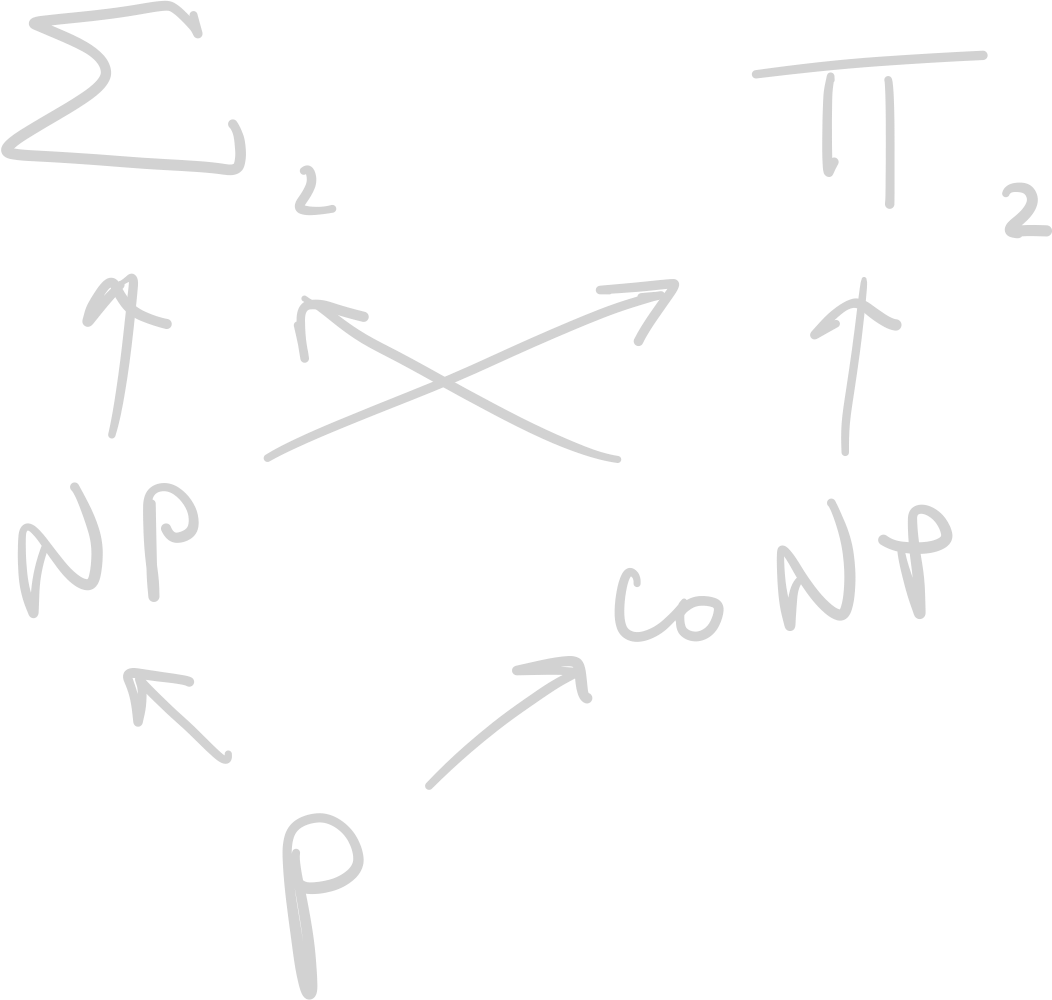
“the polynomial hierarchy is infinite”—that is, each arrow to a harder language is strict.
\(P \neq NP\), \(NP \neq \pi_{2}\)
PSPACE bounds the entire hierarchy
\(\text{PH} \subseteq \text{PSPACE}\)
because for every \(\exists\) you only have to keep one of it around.
polynomial hierarchy collapses
\(\text{P} = \text{NP} \implies \text{P} = \text{PH}\)
“the polynomial hierarchy collapses to \(P\)” We study PH because it captures problems that are solvable efficiently if \(\text{P} = \text{NP}\).
Recall–if \(\text{P} = \text{NP}\), then \(\text{P} = \text{NP} = \text{coNP}\). The fact that \(\text{P} = \text{NP}\) lets you remove a quantifier, be it exists because \(\text{P} = \text{NP}\) for all. Our claim is that:
\(\text{P} = \text{NP}\), then \(\text{ECLIQUE} \in P\). Recall ECLIQUE
Recall ECLIQUE can be written as:
\begin{align} &\exists S \subseteq V, |S| = k, \text{ s.t. $S$ is k-clique} \\ &\forall S’ \subseteq V, |S’| = k+1, \text{ s.t. $S’$ is not k-clique} \end{align}
to show the collapse, we define an “inner language” which captures the second half of this expression:
\begin{equation} \text{MQ} = \qty {\langle G,S,k \rangle, \forall S’ \subseteq V, |S’| = k+1, S \text{ is clique, $S’$ is not, $| S | = k$}} \end{equation}
MQ is the language with a poly-time checkable for-all, meaning its in coNP; using our assumption now, its also in P.
Therefore, we can write an equivalent ECLIQUE expression of the shape
\begin{equation} \text{ECLIQUE} = \qty {\langle G,k \rangle: \exists S \subseteq V, |S| = k, MQ\qty(G,S,k) = 1} \end{equation}
now this is in NP now, since we claim \(\text{MQ} \in P\). Finally if \(\text{NP} = \text{P}\), we see that \(\text{ECLIQUE} \in P\).
less dramatic collapse
Suppose we only have \(\Sigma_{k} = \Pi_{k}\), then \(\text{PH} = \Sigma_{k} = \Pi_{k}\) (because we can swap the last \(k\) things and start eating up the left); sketch—
\begin{equation} \exists \forall \exists \forall \exists \forall \exists \end{equation}
suppose we can swap the last 2 (i.e. \(\Sigma_{2} = \Pi_{2}\))
\begin{equation} \exists \forall \exists \forall \exists \qty(\exists \forall) \end{equation}
the two exists next to each other can be eaten up
\begin{equation} \exists \forall \exists \forall \exists \forall \end{equation}
and so on.
additional information
\(\Sigma\) and \(L\)
\begin{equation} L \in \Sigma_{2} \text{ if } \exists \text{ {polytime verifier $V$ s.t }} x \in L \Leftrightarrow \exists w_{1}\in \qty {0,1}^{\text{poly}\qty(|x|)} \forall w_{2} \in \qty {0,1}^{\text{poly}\qty(|x|)} V\qty(x, w_1, w_2) = 1 \end{equation}
\begin{equation} L \in \pi_{2} \text{ if } \exists \text{ {polytime verifier $V$ s.t }} x \in L \Leftrightarrow \forall w_{1}\in \qty {0,1}^{\text{poly}\qty(|x|)} \exists w_{2} \in \qty {0,1}^{\text{poly}\qty(|x|)} V\qty(x, w_1, w_2) = 1 \end{equation}
in general:
\begin{equation} L \in \Sigma_{k} \text{ if } \exists \text{ {polytime verifier $V$ s.t }} x \in L \Leftrightarrow \exists w_{1} \forall w_{2} … \underbrace{Q_{k}}_{\exists, \forall, \text{even or odd}} w_{k} V\qty(x, w_1, x_2, …, w_{k}) = 1 \end{equation}
\(\pi_{k}\) is just like flipped, so we have \(\forall\) first, and then \(\exists\).
observations
\begin{equation} \Sigma_{k} \subseteq \Sigma_{k+1} \end{equation}
\begin{equation} \pi_{k} \subseteq \pi_{k+1} \end{equation}
Also:
\begin{equation} \Sigma_{k} \subseteq \pi_{k+1} \end{equation}
\begin{equation} \pi_{k} \subseteq \Sigma_{k+1} \end{equation}