Regular expressions express computation as a simple, logical discretion, through closure properties (such as properties of regular languages). a family of languages which satisfy closure properties of DFA regular languages, which turns out to be exactly the set of languages that DFA and NFA both recognize.
“What is the complexity of describing the strings in a language?”
definition
Let \(\Sigma\) be an alphabet, we define the regular expressions over \(\Sigma\):
- for all \(\sigma \in \Sigma\), \(\sigma\) is a regexp
- \(\varepsilon\) (empty string) is a regexp
- \(\emptyset\) (empty set) is a regexp
If \(R_1\), \(R_2\) are regexps, then:
- \(R_1 \cdot R_2\) (concat) is a regexp
- \(R_1 + R_2\) (plus) is a regexp
- \((R_1)^{*}\) (set of all subsets)
Operator precidence:
- then . then +
additional information
regexp representing languages
The regexp \(\sigma \in \Sigma\) represents the language \(\qty {\sigma}\), the regexp \(\varepsilon\) represents the language \(\qty {\epsilon }\), the regexp \(\emptyset\) represents the language \(\emptyset\).
for \(R_1, R_2\) being regular expressions representing a particular regular language \(L_1, L_2\dots\)
- \((R_1 \cdot R_2)\) represents concatenation \(L_2 \cdot L_2\) in the language
- \((R_1 + R_2)\) represents union \(L_1 \cup L_2\) in the language
- \((R_1)^{*}\) represents the clean star of \(L_1\) in the language
L(R)
we refer \(L( R)\) to be the language that \(R\) represents.
accept
a string \(w \in \Sigma\) is accepted by \(R\) (“w matches R”) if \(w \in L( R)\).
regular expressions are equivalent to regular languages
another double containment
any regexp can be an NFA
given any regexp \(R\), we will construct an NFA such that \(N\) accepts exactly that in \(R\).
base cases: \(R\) has length \(1\); \(R = \sigma\), \(R = \varepsilon\), and \(R = \emptyset\), each of which has a NFA (only one symbol, directly to the accept state, or no accept state at all)
invariant: every regexp of length \(k\) represents some regular language
induction: consider \(R\) of length \(k+1\); here are the three possibilities: \(R = R_1 + R_2\), \(R = R_1R_2\), and \(R = (R_{1})^{*}\), where all \(|R_{j}| \leq |k|\). note that this means that each of the mappings map directly to a properties of regular languages (union theorem, concatenation theorem, clean star) respectively.
any NFA can be a regexp
remove states and re-labeling arcs with regular expressions—meaning we can then read substrings at a time; this operation gives us a Generalized NFA—
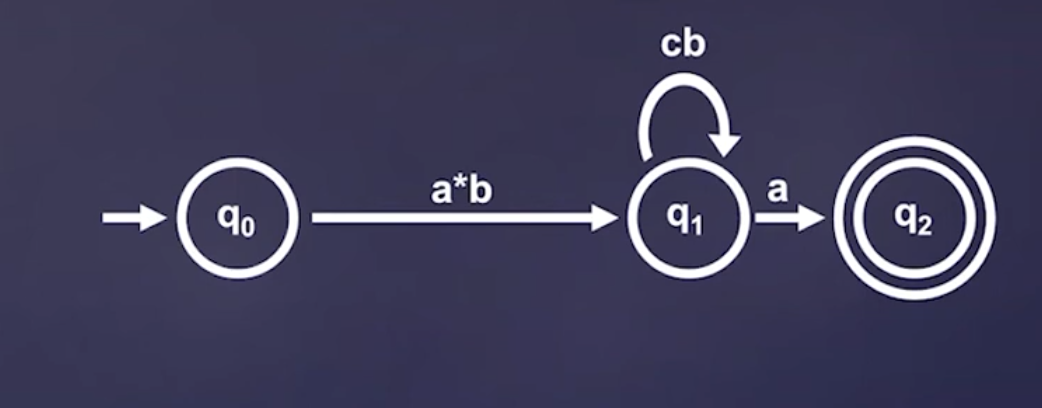
each edge can read not just a single symbol, but any string that corresponds to a regular expression
proof idea: constructions

- add unique start and accept states
- for every path of length 2 that goes between the unique start and end states, pick and internal state, rip it out, and re-label arrows