The second moment of area is a value which—given an origin—describes how point masses are distributed around that origin. (i.e. a number for how point masses are distributed). It is in units \(m^{4}\).
Take, for instance, the following picture:
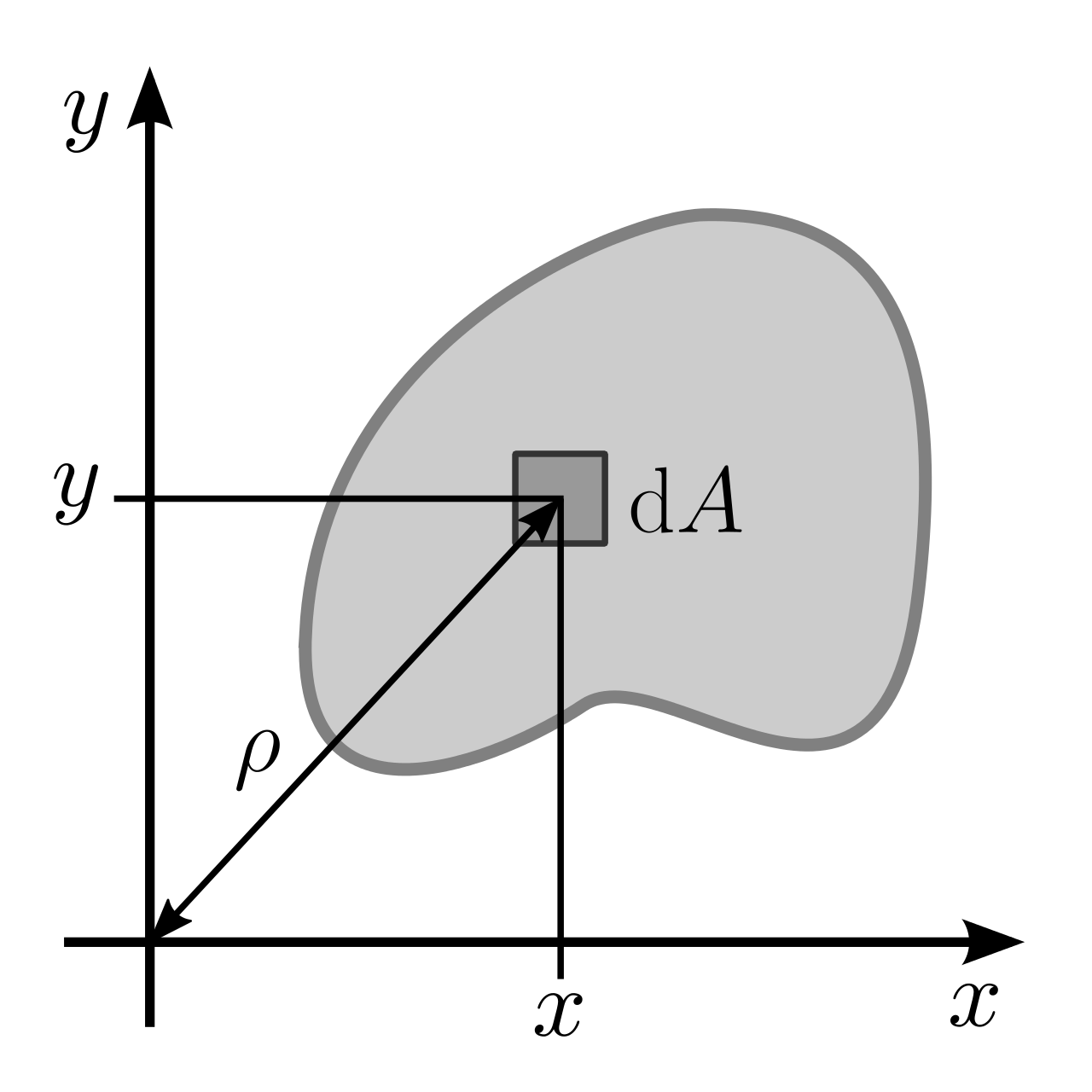
We have defined an origin at \((0,0)\) of the figure above. Furthermore, we have some \(\rho_{i}\) which is the distance from that origin to each of the infinitesimal areas \(\dd{A}\).
Then, the second moment of area is defined as:
\begin{equation} I = \iint_{R} \rho^{2} \dd{A} \end{equation}
This… would make sense.