A Social Network is a scheme for studying the relationships and interactions amongst groups of people.
- people: \(V\)
- relationship: \(E\)
- system: a network \(G(V,E)\)
Importantly, the “labels” of \(E\) often do not matter as we frequently want to study only the graphical structure of the Social Network.
degree (node)
The degree of a node is the number of edges that are touching that node (whether in or out, or undirected).
The in-degree and out-degree are the number of edges touching that node (going in or out) respectively.
degree of node
many nodes on the internet have fairly low degree, whereas some hubs have very high degree. Consider a function \(P(k)\), representing the number of nodes with degree \(k\). This follows a power law:
\begin{equation} P(k) \propto k^{-a} \end{equation}
meaning:
\begin{equation} P(k) = ck^{-a} \end{equation}
whereby as degree increases, the percentage of nodes with that number of degree drops of exponentially.
A power law distribution is log-log linear, and is “scale free”: meaning no matter how the input \(x\) is scaled its simply resulting in a multiplicative constant under the output: shape does NOT change.
Zipf’s Law
\begin{equation} freq(w_{r}) \prop \frac{1}{r^{\beta}} \end{equation}
where \(\beta\) is close to \(1\) and \(w_{r}\) is the r-th most frequent word.
betweenness
the betweenness of a target node is calculated as: for all pairs of nodes on the graph that is not our target node, what’s the ratio between the number of shortest paths between the two nodes and the number that goes through \(j\).
Formally:
for some node \(j\) for which we want to calculate betweenness, and \(s_{ik}(j)\) being the number of shortest paths between \(i\) and \(k\) that goes through \(j\) and \(s_{ik}\) being the number of shortest paths there are in general, we have:
\begin{equation} b_{j} = \frac{\sum_{i=1}^{n} \sum_{k=1}^{n} s_{ik}(j)}{\sum_{i=1}^{n} \sum_{k=1}^{n} s_{ik}} \end{equation}
where \(i \neq j \neq k\)
Recall that with directed graphs we may need to double count.
clustering coefficient
for some node \(A\), the clustering coefficient measures the percentage of nodes directly adjacent to \(A\) which are also directly adjacent with each other.
recall that, if a node has \(n\) friends, the total possible edges is \(\frac{n\qty(n-1)}{2}\).
Milgram Small-World experiment
made 300 people in Omaha NE to mail a thing to somebody in Boston by passing it through only people they knew by first-name basis.
Small World Graph
The world is a Small World Graph: networks of friends is large, sparse, decentralized, and extremely clustered. Yet, people mostly seem to be about 5-6 degrees of separation away.
This characterizes a Small World Graph:
- high clustering coefficient
- low average shortest path
Watts and Strogatz
Watts and Strogatz proposes a way to build a Small World Graph:
- start with a ring and connect each node to the next \(z\) nodes
- with probability \(p\) on each node, rewire every edge/add a shortcut to a random node
as long as \(0 < p < 1\), we get a Small World Graph
intuition: a single random connection builds a shortcut through highly centralized clusters—high \(C\), low \(L\).
weak link
most job referrals were through personal contacts, but they are often WEAK LINKS.
Triadic Closure
If two people have a common friend, its likely that they become friends eventually too. This increases cluster coefficient.
Strong Triadic Closure
If there is a strong tie between \(A - B\), and \(B - C\), then there must be a strong tie between \(A - C\).
If this property is satisfied, then any Local Bridge must be a weak tie. Otherwise:
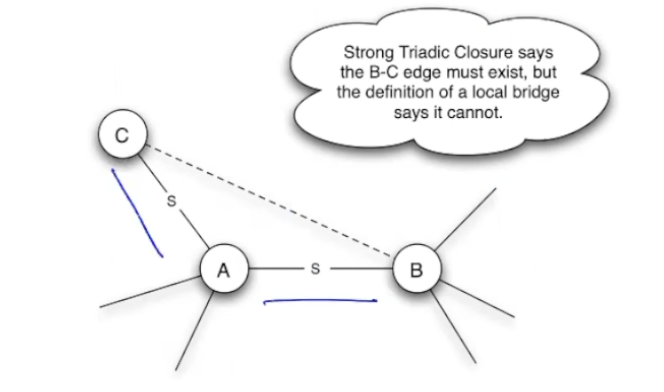
if there is a strong \(A-B\) tie and it is a local bridge, then \(C-B\) must be a connection under Strong Triadic Closure. yet, \(A-B\) is a local bridge.
By contradiction, \(A-B\) is a weak tie.
Local Bridge
A Local Bridge is an edge \(x-y\) which bridges two “local components” together. More formally, an edge between \(A,B\) is a Local Bridge if it does not live on any triangle of \(A\) or \(B\).