Today’s lambda calculus
| e → x | λx:t.e | e e | i | e + e |
why static typing?
- find type errors when the program is written
- …which makes guarantees for all possible executions
- …which can leads to a faster execution because you don’t have to do runtime type checks (this is actually non-trivial!)
why (not) static typing
- you can detect type errors during execution—so it can be sound as well
- this is not untyped: you can still have types (untyped is raw bits)
implementation
every value has a “tag” — for instance, integers vs. functions
notice that in dynamic typing function doesn’t have grantees about what the domains/ranges are, unlike static typing
basic idea: whenever you are doing something that requires a certain input type, we then check the tag. then, we emit code by taking the tag off, and then perform the operation.
dynamically typed lambda calculus
user:
| e → x | λx.e | e e | i | e + e |
runtime:
we perform tagging then at runtime
| e → x | λx.e | e e | i | e + e | !t e | ?t e |
|---|---|---|---|---|---|---|
| t → int | fun |
- where
!t eis to markewith tagt - where
?t eis to checketo have tagt, and if so we remove the tag
inference rules
dynamic type rules: first perform translation
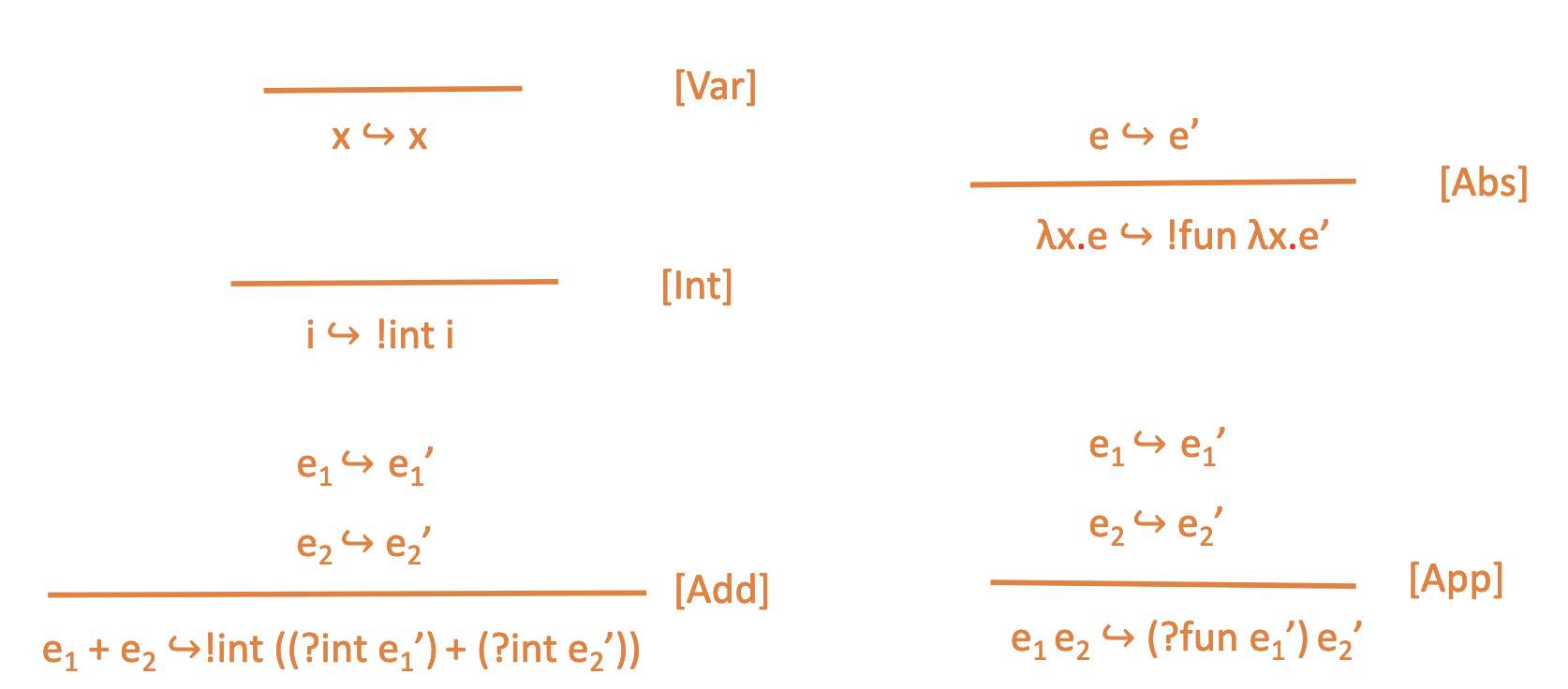
- to tag something, you steal the low-order bit from the integer
- you will take that bit as
0(this is just because addition will leave these bit)
you will notice that there is a condition for every single addition—this means that this is horrendously slow
execution rules: once translated, we now execute; in addition to standard Lambda Calculus execution rules as in structural operational semantics

This means that the specific program execution is type correct: no type checker is nagging you, so arbitrary coding is much easier! It makes as lower barrier to entry for programmers.
Debate
- safety: proving safety of all executions vs. one execution
- productivity: writing some programs vs. all programs
- performance: slower compile faster run vs. faster compile slower run
Observations
- as program size grows + number of programmers involved, static typing is better
Gradual Typing
i.e. mypy has type errors!
n = 1
n = 'x' # type error!
n: Any = 1
n = 'x'
n = a # no type error
n = n + 1 # runtime type limit
Any is a big deal: it changes the character of your type system to be mostly dynomic and require tagging.
subtyping
normal subtyping
- when
Binherits fromA, we call \(B \leq A\) - so anywhere
Ais expectedBcan be used
structural subtyping
“duck typing”
- when
Bjust so happens to implement every method fromA, we call \(B \leq A\) - so we can pass an
Bto naywhere that expects anA
uses
whether its nominal or structural, the end result is roughly the same; however, the semantics feels really different
Object
Object is the root class of the type hierarchy.
\begin{equation} \text{C} \leq \text{Object} \end{equation}
for any class \(C\).
Object is not Any, however, because Any is a generic type
Covariance
Type constructor C[A] is “covariant” if \(X \leq Y \implies C[X] \leq C[Y]\)
covariance of list
lists are NOT COVARIANT; even if \(X \leq Y\), we don’t have that \(\text{List}[X] \leq \text{List}[Y]\)
def tmp(l: List[Supertype]) -> None:
l.append(Supertype())
cp : List[Subtype] = []
tmp(cp)
cp[0].subtype_method() # crash
this gets at a heart of a central issue
- aliasing is a symmetric relationship
- subtyping is not a symmetric relationship
so, you could read something as one type and read it out another place as another type. hence, mutable types in general are not covariant.
hence, on container, we have that:
\begin{equation} \text{List}\qty(x) \leq \text{List}\qty(y) \Leftrightarrow x = y \end{equation}
Contravariant
Function types are contravariant in the domain, covariant in the range
\begin{equation} \text{Point} \to \text{Int} \leq \text{Colorpoint} \to \text{Int} \end{equation}
contravariance: \(A \to B \leq C \to D\) if \(C \leq A\) and \(B \leq D\)