Convolutional Code
A Convolutional Code, at each time \(j\), takes bit \(b_{j}\) and output two bits \(p_{2j-1}\), \(p_{2j}\), by using \(b_{j}\) and the previous two its \(b_{j-1}\) and \(b_{j-2}\).
Working Example
Consider that if you have \(k\) bits to communicate to the receiver:
\begin{equation} b_1, b_2, \dots, b_{k} \end{equation}
Codewords/Output sequence:
\begin{equation} p_1, p_{2}, \dots \end{equation}
Let we have some sequence of \(k\) input bits
\begin{equation} j = 1, \dots, k \end{equation}
then, for every input bit, we generate two output bits:
\begin{equation} p_{2j-1} = b_{j} \oplus b_{j-1} \oplus b_{j-2} \end{equation}
\begin{equation} p_{2j} = b_{j} \oplus b_{j-2} \end{equation}
if we are at \(j=1\), then we assume that \(b_{j-1} = b_{j-2} = 0\).
Shift Register
So you can encode this in a streaming fashion, and shift them off as you go
FST
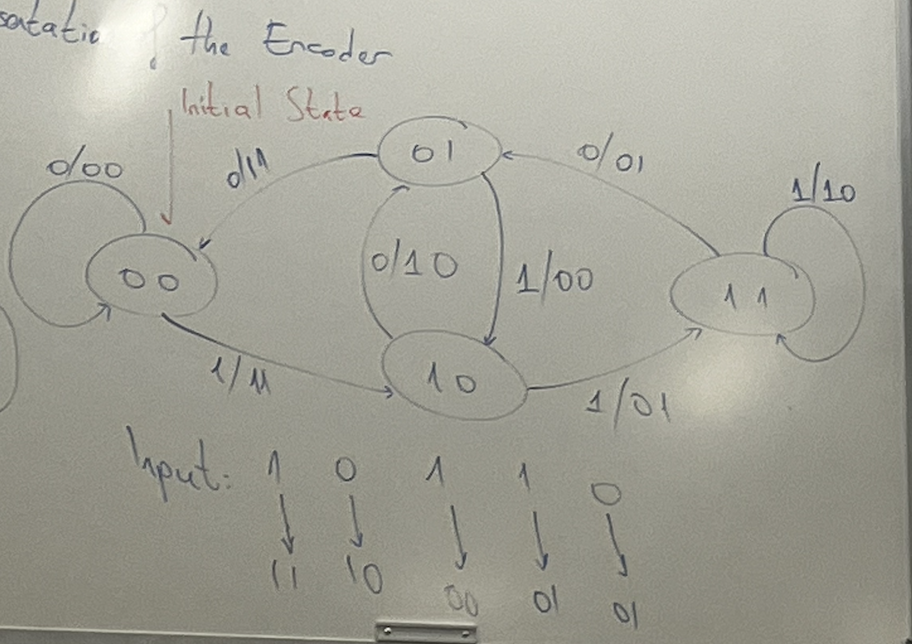
The Convolutional Code, then, is essentially a finite state machine: whereby the last two bits are essentially the “state” of the machine used for the output. \((b_{j-1}, b_{j-2})\). The input would be \(b_{j}\), and the output is \(p_{2j-1}, p_{2j}\).
During each action \(b_{j}\), we essentially perform the “shift” operation.
Therefore, you can draw it in terms of a finite state diagram.
Trellis
Now, consider rolling out finite state machine over time: make a grid of \(j\) on the x axis, and state on y axis. Then, you can trace possible lines connecting everything.
We can encode any encoding process as a PATH is the rollout trellis.
This could also help us perform decoding, because we can spot which edge our scheme traveled down.
Viterbi Decoding
bottom-up DP
- go through your edges, calculating Hamming Distance of each edge of your trellis’ decoding and the one you recieved; replace each edge with that distance
- edit distance minimize lol through the path to solve (i.e. run dijikstra on these edges)