Questions of Uniqueness and Existance are important elements in Differential Equations.
Here’s a very general form of a differential equations. First, here’s the:
function behavior tests
continuity
Weakest statement.
A function is continuous if and only if:
\begin{equation} \lim_{x \to y} f(x) =f(y) \end{equation}
Lipschitz Condition
Stronger statement.
The Lipschitz Condition is a stronger test of Continuity such that:
\begin{equation} || F(t,x)-F(t,y)|| \leq L|| x- y|| \end{equation}
for all \(t \in I\), \(x,y \in \omega\), with \(L \in (0,\infty)\), named “Lipschitz Constant”, in the dependent variable \(x\).
Reshaping this into linear one-dimensional function, we have that:
\begin{equation} \left | \frac{F(t,x)-F(t,y)}{x-y} \right | \leq L < \infty \end{equation}
The important thing here is that its the same \(L\) of convergence \(\forall t\). However, \(L\) may not be stable—in can oscillate
Differentiable
We finally have the strongest statement.
\begin{equation} \lim_{x \to y} \frac{f(x)-f(y)}{x-y} = C \end{equation}
To make something Differentiable, it has to not only converge but converge to a constant \(C\).
Existence and Uniqueness Check for differential equation
Assume some \(F:I \times \omega \to \mathbb{R}^{n}\) (a function \(F\) whose domain is in some space \(I \times \omega\)) is bounded and continuous and satisfies the Lipschitz Condition, and let \(x_{0} \in \omega\), then, there exists \(T_{0} > 0\) and a unique solution for \(x(t)\) that touches \(x_{0}\) to the standard First-Order Differential Equation \(\dv{x}{t} = F(t,x), x(t_{0}) = t_{0}\) for some \(|t-t_{0}| < T_{0}\).
To actually check that \(F\) satisfies Lipschitz Condition, we pretty much usually just go and take the partial derivative w.r.t. \(x\) (dependent variable, yes its \(x\)) of \(F\) on \(x\), which—if exists on some bound—satisfies the Lipschitz condition on that bound.
Proof
So we started at:
\begin{equation} \dv{x}{t} = F(t,x), x(t_{0}) = x_{0} \end{equation}
We can separate this expression and integrate:
\begin{align} & \dv{x}{t} = F(t,x) \\ \Rightarrow\ & \dd{x} = F(t,x)\dd{t} \\ \Rightarrow\ & \int_{x_{0)}}^{x(t)} \dd{x} = \int_{t_{0}}^{t} F(s,x(s)) \dd{s} \\ \Rightarrow\ & x(t)-x_{0}= \int_{t_{0}}^{t} F(s,x(s)) \dd{s} \end{align}
At this point, if \(F\) is seperable, we can then seperate it out by \(\dd{t}\) and taking the right integral. However, we are only interested in existance and uniquness, so we will do something named…
Picard Integration
Picard Integration is a inductive iteration scheme which leverages the Lipschitz Condition to show that a function integral converges. Begin with the result that all First-Order Differential Equations have shape (after forcibly separating):
\begin{equation} x(t)-x_{0}= \int_{t_{0}}^{t} F(s,x(s)) \dd{s} \end{equation}
We hope that the inductive sequence:
\begin{equation} x_{n+1}(t) = x_{0} + \int_{t_{0}}^{t} F(s,x_{n}(s)) \dd{s} \end{equation}
converges to the same result above (that is, the functions \(x_{n}(s)\) stop varying and therefore we converge to a solution \(x(s)\) to show existance.
This is hard!
Here’s a digression/example:
if we fix a time \(t=10\):
we hope to say that:
\begin{equation} \lim_{n \to \infty } G_{n}(10) = G(10) \end{equation}
\(\forall \epsilon > 0\), \(\exists M < \infty\), \(\forall n>M\),
\begin{equation} |G_{n}(10)-G(10)| < \epsilon \end{equation}
Now, the thing is, for the integral above to converge uniformly, we hope that \(M\) stays fixed \(\forall t\) (that all of the domain converges at once after the same under of the iterations.
Taking the original expression, and applying the following page of algebra to it:
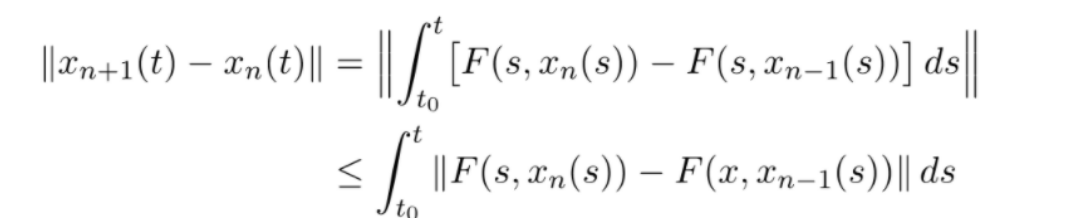
Finally, we then apply the Lipschitz Condition because our setup is that \(F\) satisfies the Lipschitz Condition, we have that:
\begin{equation} ||x_{n+1}(t)-x_{n}(t)|| \leq L\int_{x_{0}}^{t} ||x_{n}(s)-x_{n-1}(s)||ds \end{equation}
