value iteration, in practice

Say we have a system:

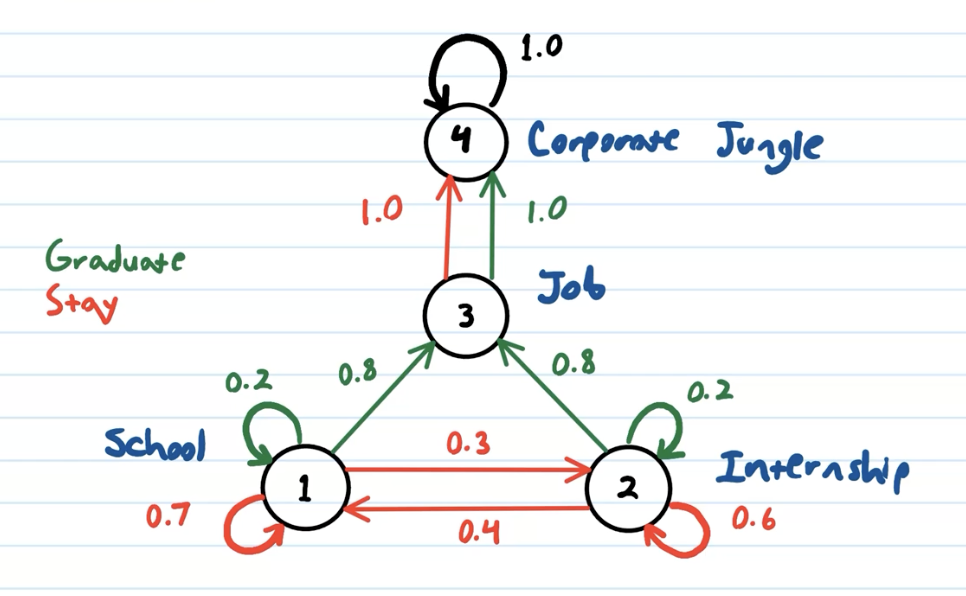
1. States: 4—school, internship, job, jungle
2. Actions: 2—stay, graduate

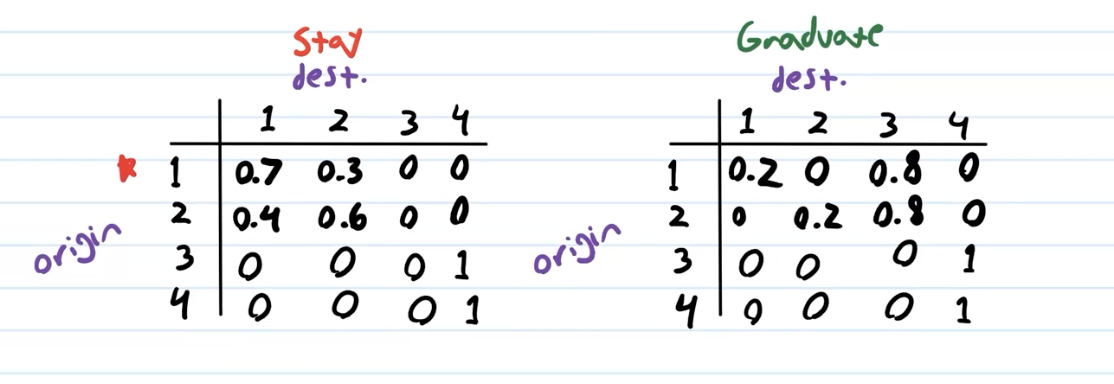
create transition model

Create tables of size \(S \times S\) (that is, 4x4), one for each action. These are our transition models. Rows are the states where we took the action, columns are the states which are the results of the action, and the values are the probability of that transition happening given you took the action.

Each row should sum up to \(1\): after an action, you should always end up at some state.

enumerate rewards and discount

for us, we are going to say that:

• \(R(s_1)= -1\)
• \(R(s_2)= +1\)
• \(R(s_3) = +5\)

the rest of this should work if your states are parameterized by action.

We are going to discount by \(0.9\)

iterate!

1. for each state…
   1. calculate the values within the sum of the Bellman update for each action as well as the instantaneous reward for being in that state
   2. get the maximum value of that
   3. store for the next iteration